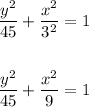ANSWER:
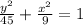
Explanation:
We can notice from the foci and covertice two things, the first is that the center of the ellipse is at the origin and that the major axis is the vertical axis.
Thanks to this, we can establish that the equation of the ellipse in its standard form is the following:
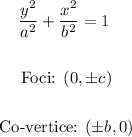
That is to say, that we know the value of b and c, we need the value of a, which we calculate by means of the Pythagorean theorem, like this:
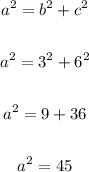
Therefore, the equation is the following: