Solution
The tailwind means the jet is flying with the wind while, the headwind means the jet is flying against the wind
We first the speed for eac case
For the Tailwind Speed (TS)
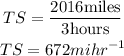
The speed of the Tailwind is 672 miles per hour
For the Headwind Speed (HS)
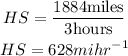
The speed of the Headwind is 628miles per hour
Now, We will now find the speed of the jet in still air as well as the speed of the wind
Let u denotes the speed of the jet in still air, and let v denotes the speed of the wind
This therefore implies that (Note: The tailwind means the jet is flying with the wind)

and (Note: the headwind means the jet is flying against the wind)
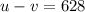
We will solve the two equation simultaneously

Equation (1) + equation (2)
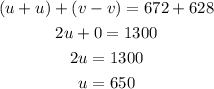
Substitute the value of u into equation (1)
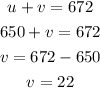
Therefore,
The speed of the jet in still air is 650 mi/hr
The speed of the wind is 22 mi/hr