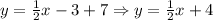Question

Use point slope form to write the lines with the given slope and point in slope intercept form. 1. m= _1/3 (-3,5) 2. m = 1/2 (6,7)

Answer 1

We need to use the formula:

`y-y_1=m(x-x_1)`

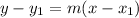
To write the lines with the given slope and point to find the slope-intercept form of the line. Then, we have:

1. First equation:

m = -1/3, (-3, 5) ---> x1 = -3, y1 = 5

`y-5=-(1)/(3)(x-(-3))\Rightarrow y-5=-(1)/(3)(x+3)=-(1)/(3)x-(3)/(3)`

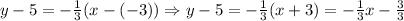
Then, we have:

`y-5=-(1)/(3)x-1\Rightarrow y=-(1)/(3)-1+5\Rightarrow y=-(1)/(3)x+4`

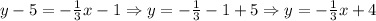
Hence, the slope-intercept form for the line is:

`y=-(1)/(3)x+4`

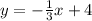
2. Second equation:

m = 1/2, (6, 7) ---> x1 = 6, y1 = 7

Then, we have

`y-7=(1)/(2)(x-6)=(1)/(2)x-(6)/(2)=(1)/(2)x-3\Rightarrow y-7=(1)/(2)x-3`

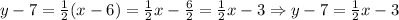
Therefore, the slope-intercept form for the line is:

`y=(1)/(2)x-3+7\Rightarrow y=(1)/(2)x+4`