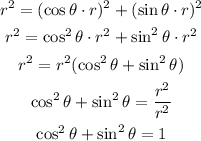Question

Consider the right triangle shown below.Use the Pythagorean Theorem to write an equation relating x, y, and r.   Write a formula that expresses x in terms of r and θ.x=Write a formula that expresses y in terms of r and θ.y=Use your answers to parts (a)-(c) to write an equation relating cos(θ), sin(θ), and r.

Answer 1

`\begin{gathered} r^2=x^2+y^2 \\ x=\cos \theta\cdot r \\ y=\sin \theta\cdot r \\ \cos ^2\theta+\sin ^2\theta=1 \end{gathered}`

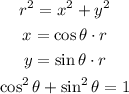
Explanation:

a.

The Pythagorean theorem says the following:

`\begin{gathered} c^2=a^2+b^2 \\ a=x \\ b=y \\ c=r \\ \text{replacing:} \\ r^2=x^2+y^2 \end{gathered}`

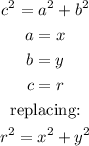
b.

The trigonometric function that relates these values is the cosine, which is given as follows

`\begin{gathered} \cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}} \\ \text{adjacent = x} \\ \text{hypotenuse = r} \\ \text{replacing:} \\ \cos \theta=(x)/(r) \\ x=\cos \theta\cdot r \end{gathered}`

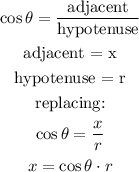
c.

The trigonometric function that relates these values is the sine, which is given as follows

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \text{opposite}=y \\ \text{hypotenuse}=r \\ \sin \theta=(y)/(r) \\ y=\sin \theta\cdot r \end{gathered}`

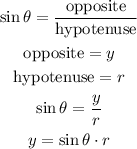
d.

We replace x and y obtained at point b and c in the equation at point a, just like that

`\begin{gathered} r^2=(\cos \theta\cdot r)^2+(\sin \theta\cdot r)^2 \\ r^2=\cos ^2\theta\cdot r^2+\sin ^2\theta\cdot r^2 \\ r^2=r^2(\cos ^2\theta+\sin ^2\theta) \\ \cos ^2\theta+\sin ^2\theta=(r^2)/(r^2) \\ \cos ^2\theta+\sin ^2\theta=1 \end{gathered}`