Answer:
1.0
Explanation:
To find the variance of the probability distribution, we make use of the formula:
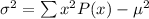
First, find the expected value, i.e mean of the distribution.
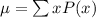
From the table, the mean of the distribution = -0.60.
Next, we find the variance.
From the table:
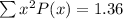
Therefore:
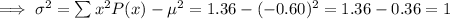
The variance of the probability distribution is 1.0