To determine the probability using a normal approximation we need to determine the z-score of the sample. To do that we use the following formula:

Where:
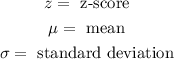
First, we need to calculate the mean. To do that we use the following formula:

Where
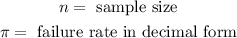
To determine the decimal form of the failure rate we divide the percentage by 100, like this:
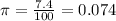
The sample size, in this case, is 295. Substituting we get:
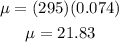
Now, we need to calculate the standard deviation. We do this using the following formula:

Substituting the values we get:
![\sigma=\sqrt[]{(295)(0.074)(1-0.074)}](https://img.qammunity.org/2023/formulas/mathematics/college/jpdcst49w65fy1j9l964hd3sxfkaukjcg1.png)
Solving the operations:
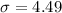
Since we are approximating to binomial we need to use a continuity correction factor of 0.5 to the number of chips we are considering. Let "x" be the number of chips, we have that:
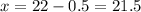
Now we substitute in the formula for the z-score:

Now, we solve the operations:
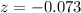
Therefore, in the binomial distribution, we need to determine the area for z = -0.073. Therefore, the probability is:

Therefore, the probability is 0.472