Question

The image of point (4,-9) under a translation is (9,-14). Find the coordinates of the point (-9,-8) under the same translation

Answer 1

First, you have to find the translation made to (4,-9) to determine the point (9,-14). You can plot both points to see their positions in the coordinate system

As you can see, the image (9,-14) is to the right and downwards of the preimage (4,-9), this means that the point was moved to the right and down.

- To make a horizontal movement to the right, you have to add a constant "c" to the x-coordinate of the point, following the rule:

`(x,y)\to(x+c,y)`

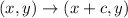
To determine the value of the constant, you have to compare the x-coordinates of both points:

`4+c=9`

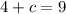
Subtract 4 to both sides of the expression

`\begin{gathered} 4-4+c=9-4 \\ c=5 \end{gathered}`

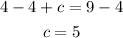
The point was moved 5 units to the right.

- To make a vertical translation down, you have to subtract a constant "k" to the y-coordinate of the point, following the rule

`(x,y)\to(x,y-k)`

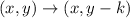
To determine the number of units of the vertical translation, you have to compare the y-coordinates of both points:

`-9-k=-14`

Add 9 to both sides of the expression

`\begin{gathered} -9+9-k=-14+9 \\ -k=-5 \end{gathered}`

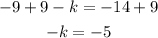
Multiply both sides by -1 to change the sign:

`\begin{gathered} (-1)(-k)=(-1)(-5) \\ k=5 \end{gathered}`

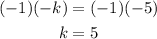
The point was moved 5 units down.

Next, you have to apply the same translation to point (-9,-8), as mentioned, the point was moved 5 units to the right and 5 units down, the translation rule is:

`(x,y)\to(x+5,y-5)`

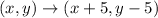
Add 5 to the x-coordinate and subtract 5 to the y-coordinate:

`(-9,-8)\to(-9+5,-8-5)=(-4,-13)`

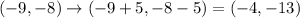
The image of the point (-9,-8) after the transformation will be (-4,-13)