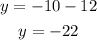Question

How do I solve a function table and write the function rule

Answer 1

`\begin{gathered} y=x-12 \\ y=-6,x=6 \\ x=-10,y=-22 \end{gathered}`

Step-by-step explanation

The first step is to find the equation that represents the function given.

The function is a linear function. The general form of a linear function is given as:

`y=mx+b_{}`

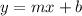
where m = slope; b = y intercept

To find the slope, we can apply the formula:

`m=(y_2-y_1)/(x_2-x_1)`

where (x₁, y₁) and (x₂, y₂) are two sets of data points from the table

Let us pick (32, 20) and (14, 2) as (x₁, y₁) and (x₂, y₂).

Therefore:

`\begin{gathered} m=(2-20)/(14-32) \\ m=(-18)/(-18) \\ m=1 \end{gathered}`

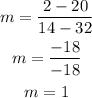
Now, find the function by using the point-slope method:

`y-y_1=m(x-x_1)`

Therefore:

`\begin{gathered} y-20=1(x-32) \\ y-20=x-32 \\ y=x-32+20 \\ y=x-12 \end{gathered}`

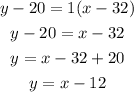
That is the rule/function that represents the table.

To find the value of x when y is -6, substitute y with -6 in the function above and solve for x:

`\begin{gathered} -6=x-12 \\ \Rightarrow x=-6+12 \\ x=6 \end{gathered}`

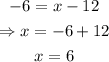
To find the value of y when x is -10, substitute x with -10 in the function and solve for y:

`\begin{gathered} y=-10-12 \\ y=-22 \end{gathered}`