Question

A +6 nC charge is located at (0,8.44) cm and a -4nC charge is located (3.12, 0) cm.Where would a -10 nC charge need to be located in order that the electric field at the origin be zero? Find the distance r from the origin of the third charge.

Answer 1

The electric field exerted by a point charge is given by:

`E=k(q)/(r^2)`

where q is the charge and r is the distance to the point where we want to calculate the electric field.

In this case we have three charges with the following properties:

`\begin{gathered} q_1=6*10^(-9),\text{ }r_1=0.0844 \\ q_2=-4*10^(-9),\text{ }r_2=0.0312 \\ q=-10*10^(-9),\text{ }r \end{gathered}`

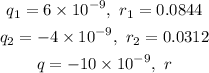
Now, the total electric field on a point is the addition of all the charges; in this case we want the net field to be zero. Then we have:

`\begin{gathered} k(6*10^(-9))/((0.0844)^2)-k(4*10^(-9))/((0.0312)^2)-k(10*10^(-9))/(r^2)=0 \\ (10)/(r^2)=(6)/((0.0844)^2)-(4)/((0.0312)^2) \\ (10)/(r^2)=-3266.84 \\ r^2=-(10)/(3266.84) \end{gathered}`

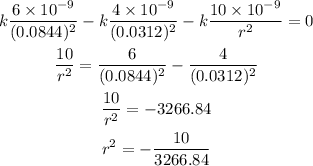
Now, since the last equation does not have a real solution this means that this distribution of charges will not exert a zero electric field on the origin.

Therefore, there's no possible distance for the field to be zero in this charge configuration