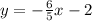
Check the graph below, please
1) Since we have the equation in the Standard form we can manipulate it so that we can have the slope-intercept form:
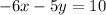
Let's isolate the y-term on the left:
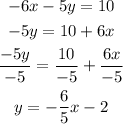
2) Now, let's plot the line of this function, by picking values for x and inserting them to get the value of y. We can write out the T table:
x|y
-1y=-6/5(-1)-2 => y=-0.8
0 | -2
1 |-3.2
With the points (-1, -0.8), (0,-2) and (1,-3.2) we can trace a decreasing line:
for the slope m is negative.
3) Hence, these are the answers above: