The function is given to be:
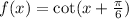
A full period of a tan graph is π. Hence, we will make sure our table of values will cover more than π units for the x-axis.
To get the first value we can use in the table of values, we will equate the function to 0 and solve for x:

We will take intervals of π/6, such that we will use values of x to be:
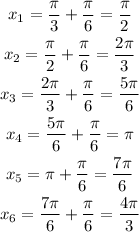
If we substitute these values into the function, we can prepare a table as shown below:
Note that there is a vertical asymptote at x = 5π/6.
Using this table, the graph is drawn as shown below: