Question

A man is changing a light bulb at the top of a 1500 foot tall radio tower and drops his screwdriver.  Assuming no air resistance, how long will it take to hit the ground in seconds?

Answer 1

The time it takes for the screwdriver to hit the ground is approximately 11.64 seconds.

Step-by-step explanation:

Assuming no air resistance, the time it takes for an object to fall to the ground can be determined using the time of flight formula:

t = √((2h)/g)

Where t is the time of flight, h is the height of the tower, and g is the acceleration due to gravity.

Plugging in the values from the question, the time it takes for the screwdriver to hit the ground is:

t = √((2 * 1500 feet) / (32.2 ft/s^2))

t ≈ 11.64 seconds

Answer 2

9.68 seconds

Step-by-step explanation:

To answer the question, we will use the following equation for the uniformly accelerated motion:

`x=v_0t+(1)/(2)at^2`

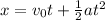
Where x is the distance travel by the object, v0 is the initial velocity, a is the acceleration and t is the time.

Since, the man drops his screwdriver, x = 1500 ft, v0 = 0 ft/s and a = -32 ft/s².

Then, replacing the values, we get:

`\begin{gathered} -1500=0t+(1)/(2)(-32)t^2 \\ -1500=(1)/(2)(-32)t^2 \end{gathered}`

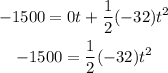
Then, solving for t, we get:

`\begin{gathered} -1500=-16t^2 \\ (-1500)/(-16)=(-16t^2)/(-16) \\ 93.75=t^2 \\ \sqrt[]{93.75}=t \\ 9.68\text{ s = t} \end{gathered}`

Therefore, the screwdriver takes 9.68 seconds to hit the ground.