From the circle;
We are to find the length of arc FGE
Given
Radius of circle = 10
From the circle
The reflex angle is
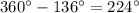
Therefore the reflex angle = 224
We will calculate length of arc FGE using
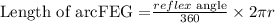
Substituting values we get
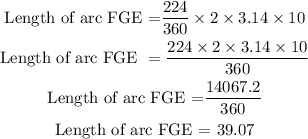
Therefore the length of arc FGE is 39.1 to the nearest tenth