Answer:
Cost of one slice of cheese pizza = $1.50
System of equations;
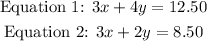
Step-by-step explanation:
Let x represent the cost of one slice of cheese pizza.
Let y represent the cost of one slice of mushroom pizza.
So if Jack bought 3 slices of cheese pizza and 4 slices of mushroom pizza for a total cost of $12.50, we can express this as;

And if Grace bought 3 slices of cheese pizza and 2 slices of mushroom pizza for a total cost of $8.50, we can express this as;

We can now solve both equations simultaneously using the elimination method.
Subtracting equation 2 from equation 1, we'll have;
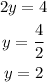
To find x, let's put y = 2 into Equation 1 and solve for x;
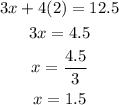
We can see that the cost of one slice of cheese pizza is $1.50.