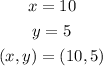Question

using the elimination method, find x and y: please explain to me, I want an explanation because I don't get this a 100% yet 4x - 3y = 25-3x + 8y = 10

Answer 1

Given the system of equations :

`\begin{gathered} 4x-3y=25 \\ -3x+8y=10 \end{gathered}`

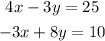
To eliminate y :

multiply the first equation by 8 and the second equation by 3

`\begin{gathered} 8\cdot4x-8\cdot3y=8\cdot25 \\ 3\cdot-3x+3\cdot8y=3\cdot10 \\ ================ \\ 32x-24y=200 \\ -9x+24y=30 \end{gathered}`

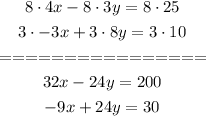
Add the equation , we will find the sum of y = 0

`\begin{gathered} (32x-24y)+(-9x+24y)=200+30 \\ 32x-24y-9x+24y=230 \\ (32x-9x)+(-24y+24y)=230 \\ (23x)+(0)=230 \end{gathered}`

So, solve the the result for x

`\begin{gathered} 32x-9x=200+30 \\ 23x=230 \\ \\ x=(230)/(23)=10 \end{gathered}`

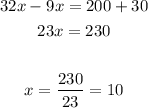
Then substitute with x at the first equation to find y

`\begin{gathered} 4\cdot10-3y=25 \\ 40-3y=25 \\ -3y=25-40 \\ -3y=-15 \\ \\ y=(-15)/(-3)=5 \end{gathered}`

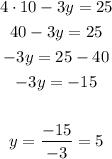
So, the answer of the system of equations :

`\begin{gathered} x=10 \\ y=5 \\ (x,y)=(10,5) \end{gathered}`