We have to graph the quadratic equation defined as:
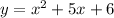
We can already identify that:
• The parabola opens upward (a > 0).
,
• The y-intercept is y = 6 (c = 6).
We can use the quadratic formula to find the roots:
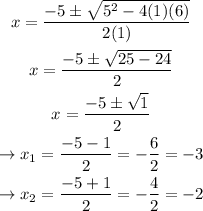
The roots are x = -3 and x = -2.
We can graph the parabola with these 3 points as:
Answer: The roots are located at x = -3 and x= -2.