Question

use the point-slope formula to write an equation of the line that passes through (-2, -4) and (4,1) .Write the answer in slope-intercept form (if possible).

Answer 1

The point-slope form of writing a line equation is given by the following generic expression:

`y-y_0=a(x-x_0)`

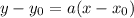
where a is the slope, and x0 and y0 is any of the points that the line passes through.

Because we have two points of the given line, we are able to calculate the slope as follows:

`\begin{gathered} a=(\Delta y)/(\Delta x)=(y_1-y_2)/(x_1-x_2) \\ \\ a=(1-(-4))/(4-(-2)) \\ \\ a=(1+4)/(4+2) \\ \\ a=(5)/(6) \end{gathered}`

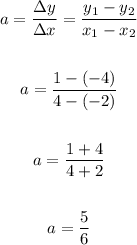
Now, by substituting it, and one of the points in the generic expression, we are able to find the following expression for the line:

`y+4=(5)/(6)(x+2)`

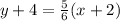
now, to write it in the slope-intercept form, we need to isolate Y and simplify the equation, as follows:

`\begin{gathered} y=(5)/(6)x+(5)/(3)-4 \\ \\ y=(5)/(6)x-(7)/(3) \end{gathered}`