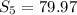Given:
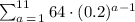
To find: Sum of first 5 terms
Step-by-step explanation:
Here, the first term is,
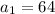
The common ratio, r = 0.2
The number of terms n = 5.
Using the sum formula for geometric series,
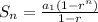
Substituting the values we get,
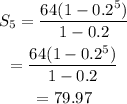
Thus, the sum of the first 5 terms is 79.97.
Final answer: