ANSWER
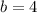
Step-by-step explanation
The two lines given are:
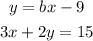
They intersect at the point (k, k). This means that at that point, they have the same values of x and y.
First, find the value of k by substituting (k, k) for (x, y) in the second equation:
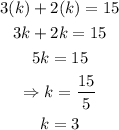
Therefore, the point they intersect is (3, 3).
To find the value of b, substitute (3, 3) for (x, y) in the first equation and simplify:
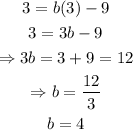
That is the value of b.