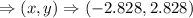Answer:
The radius is given below as
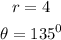
The equation of a circle is given below as
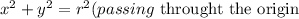
By converting the polar coordinate to rectangular coordinates, we will have
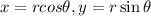
By substituting the values, we will have
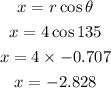
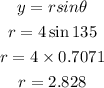
Hence,
The coordinates of the point on a circle centered at the origin with radius 4 corresponding to an angle of 135 degrees is