Step-by-step explanation
An ordered pair is a solution of a line if it "satisfies" the equation of the line. What does "satisfy" mean? It means that evaluating the pair for the point doesn't give a contradiction, but a true equality.
Now, let's test the first ordered pair:
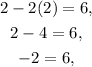
Note that after evaluating the equation of our line for (2,2) we got a contradiction: -2 is not equal to 6. This means that (2,2) is not a solution to our line.
Let's test (0,-3):
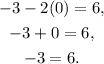
Again we got a contradiction. (0,-3) is not a solution to our line.
Let's test (-3,0):
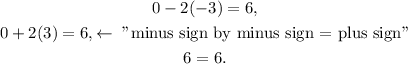
We got something true (6 is equal to itself).
Answer
The ordered pair from the options that is a solution of our line is