Answer:
x=6.21 cm
Explanation:
In the given triangle, we are required to find the length of AB, that is x cm.
First, find the value of angle ACD.
Using the Law of Sines:
![\begin{gathered} (\sin C)/(c)=(\sin A)/(a) \\ \implies(\sin C)/(15)=(\sin25\degree)/(9)\text{ where }\begin{cases}c=AD=15\operatorname{cm} \\ a=CD=9\operatorname{cm} \\ A=25\degree\end{cases} \end{gathered}]()
Multiply both sides by 15.
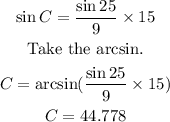
Since angle C in the figure is an obtuse angle:
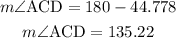
Next, we find the value of angle ADC.
In triangle ACD:
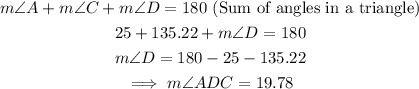
The diagram below shows the two angles.
The next step is to find the length of AC using the Law of Sines.:
![\begin{gathered} (d)/(\sin D)=(a)/(\sin A) \\ \implies(d)/(\sin 19.78\degree)=(9)/(\sin25)\text{ where }\begin{cases}D=19.78\degree \\ a=CD=9\operatorname{cm} \\ A=25\degree\end{cases} \end{gathered}]()
Multiply both sides by sin 19.78.
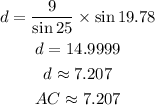
Find the value of angle ACB in triangle ABC.
The sum of angles on a straight line is 180 degrees.
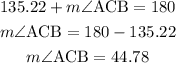
Find the value of angle ABC in triangle ABC.

From the diagram below:
Applying the Law of Sines to triangle ABC:
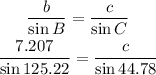
Multiply both sides by sin 44.78.
![\begin{gathered} c=(7.207)/(\sin125.22\degree)*\sin 44.78\degree \\ c=6.21\operatorname{cm} \end{gathered}]()
The length of x (i.e AB) is 6.21 cm (correct to 3 significant figures).