To factor the expression:
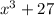
we need to notice that this is equal to:
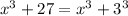
then we have a sum of cubes. A sum of cubes can always be factor as:
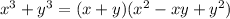
Then we can factor the expression as:

To find the roots we equal the factor expression to zero and solve for x:
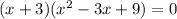
This equation implies that:
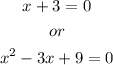
The first equation can be solved as:
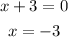
The second one can be solve as:
![undefined]()