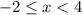Question

Solve the system of two linear inequalities graphically. Graph the solution set of the second linear inequality. Choose the type of boundary line? Enter the two points on the boundary line? Select the region you wish to be shaded?

Answer 1

Considering the system of two linear inequalities:

`\begin{cases}x<4 \\ x\ge-2\end{cases}`

The first inequality "x < 4" indicates all values of x less than 4. To graph this inequality, you have to draw a vertical line at x=4, since the symbol of the inequality does not include that equal sign, it means that 4 is not included. To represent in the graph that 4 is not included, you have to use a dashed line. After drawing the line, you have to shade the area to the left of it.

The second inequality "x ≥ -2" indicates all values greater than or equal to -2. You have to draw a solid vertical line at x=2 and shade the area to the left of the said line to represent all values greater than -2.

The solution for the system of inequalities is represented by the portion of the graph where both shades overlap

`-2\leq x<4`