The sample size of the poker is 52 ( since there 52 cards )
Since a 2, 3, 4, and 5 have been dealt, therefore the sample size will be (52 - 4 = 48)
The probability of drawing a card with the number x is
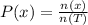
Thus, the probability of picking a six will be
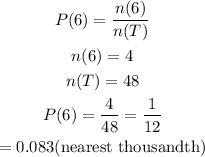
Hence, the probability that your last card is the number six is 0.083