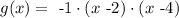Question

What is the Solution to the question of this problem

Answer 1

We want to find an equation that fits the given data.

First, as it is the easiest equation, we think of something of the form y=mx+b.

However, we see that at x=2 and x=4, the value of the function is f(x)=0. This suggests that we cannot consider a function of the form y=mx+b, as this type of equations can only have at most one value of x where the function is 0.

So, now, we think of a function of the form f(x)= ax²+bx+c, which a polynomial of degree two. This also make sense as normally this functions look like this

which means that this functions have an axis of symmetry around which the values are the same.

IN our case, we see that at x=2 and x=4, f(x)=0. At x=1 and at x=5 we have that f(x)=-3. So, it seems that the axis of symmetry is located at x=1.

Since we have a polynomial of degree 2 and we know that at x=2 and x=4 the function is 0, we can propose the following function

`f(x)=(x-2)\cdot(x-4)`

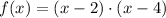
Note that at x=3 we have

`f(3)=(3\text{ -2)}\cdot(3\text{ -4) = 1}\cdot\text{ -1 = -1}`

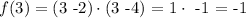
which does not correspond to the data we are given. Then, we multiply the function by -1. So we propose the function

`g(x)=\text{ -(x-2)}\cdot(x\text{ -4)}`

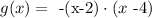
We can see that at g(2)=g(4)=0 and that g(3)=1.

Let us check that it also fulfills the other two data points

`g(1)=\text{ -1}\cdot(1\text{ -2)}\cdot(1\text{ -4)= -1}\cdot\text{ -1}\cdot\text{ (-3)= -3}`

and

`g(5)=\text{ -1}\cdot(5\text{ -2)}\cdot(5\text{ -4)= -1}\cdot\text{ 3}\cdot\text{ 1 = -3}`

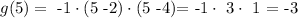
which confirms that our solution is correct. So the funciton that passes through the given points is

`g(x)=\text{ -1}\cdot(x\text{ -2)}\cdot(x\text{ -4)}`