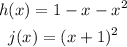
To check whether the two functions are equal, let's simplify j(x).
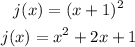
As we can see, h(x) and j(x) are not equal. We can further justify this by assuming a value of x. Let's say at x = 1.
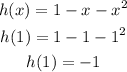
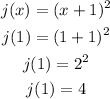
As we can see at x = 1, the value of h(x) is -1 while the value of j(x) is 4. They are not equal. In general, the two functions h(x) and j(x) are not equal.
On the other hand, at domain (0, a) or at x = 0:
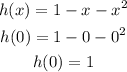
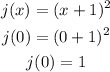
At x = 0, both functions are equal that is h(x) = j(x) = 1.