Question

Please help me !!!!!!! Amie and Taylor each wrote a function that represented the same parabola. F(x)=-(x+2)(x-4) , f(x) =-1 (x-1)^2 +9 . What are the x intercepts of the parabola ? What is the y intercept ?

Answer 1

Given the function of the parabola:

`\begin{gathered} f(x)=-(x+2)(x-4) \\ \\ f(x)=-1(x-1)^2+9 \end{gathered}`

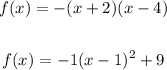
Given that both functions represent the same parabola.

Let's find the x-intercepts and y-intercept of the parabola.

The x-intercept is the point where the parabola crosses the x-axis.

Let's find the x-intercept from the first equation.

To find the x-intercept, substitute 0 for f(x) in the first function and solve.

We have:

`\begin{gathered} 0=-(x+2)(x-4) \\ \\ -(x+2)(x-4)=0 \\ \\ \end{gathered}`

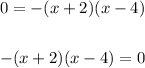
Equate each individual factor to zero:

`\begin{gathered} x+2=0 \\ x-4=0 \end{gathered}`

`\begin{gathered} x+2=0 \\ \text{Substitute 2 from both sides:} \\ x+2-2=0-2 \\ \\ x=-2 \end{gathered}`
`\begin{gathered} x-4=0 \\ Add\text{ 4 to both sides:} \\ x-4+4=0+4 \\ x=4 \end{gathered}`

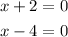
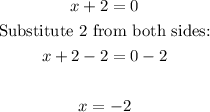
Therefore, the x-intercepts of the parabola are:

x = -2, 4

In point form, the x-intercepts are:

(-2, 0) and (4, 0)

Y-intercept:

To find the y-intercept, substitute 0 for x and solve

`\begin{gathered} f(0)=-(0+2)(0-4) \\ \\ f(0)=-(2)(-4) \\ \\ f(0)=-2(-4) \\ \\ f(0)=8 \end{gathered}`

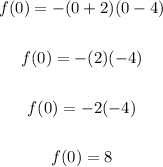
Therefore, the y-intercept is at, y = 8

In point form, the y-intercept is:

(0, 8)

ANSWER:

x-intercepts: (2, 0) and (4, 0)

y-intercept: (0, 8)