a)
We know that the distribution of the population is normally distributed with mean $6.25 and standard deviation $2.28 hence we have:
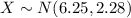
b)
We know that the standard deviation of the mean is given by:

Then in this case we have:
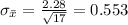
We also know that the mean of the distribution of the mean is equal to the mean of the population. Then the distribution of the mean is:
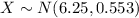
c)
If we choose a random person we would need to use the distribution in part a. We need to find the probability:
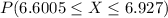
to calculate this probability, we need to standardize the distribution, we achieve this by using the z-score defined as:

Then we have:
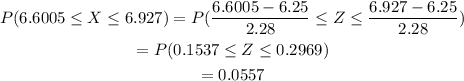
Therefore, the probability in this case is 0.0557
d)
In this case, since we are choosing from the group of 17 patrons, we will use the distribution on part b. Doing the same as the previous point we have:
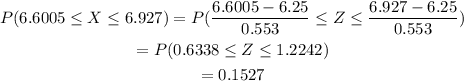
Therefore, the probability in this case is 0.1527
e)
Since the sample is less than 30, the assumption of normality is relevant, therefore, the answer is Yes