Given:
32% of people have type A blood.
To find:
Probability of a selecting person that does not having type A blood.
Step-by-step explanation:
Probability can be defined as the ratio of a number of favourable outcomes and a total number of outcomes.
Let the total number of person = 100.
As it is given that 32% of people have type A blood,

So, we can say that 32 out of 100 that having to type A blood.
Now, to find the people that does not have type A blood is:
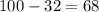
i.e., 68 people do not have type A blood.
So, the probability of selecting a person and getting someone who does not have type A blood:
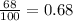
Final answer:
Hence, the required probability value is 0.68.