x=4, y=6 or ( 4,6)
1) Let's solve this by making use of the Substitution Method
3x+ 4y = 36
y= -1/2x+8
2) Plugging into the first one the 2nd equation:
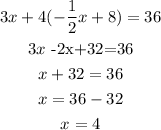
Note that we combined like terms on the 2nd line
And subtracted 32 from both sides.
2.2) Now we can plug into any of them, x=4
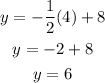
2.3) Testing those solutions we can write out:
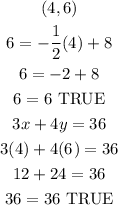
3) Hence, we can state that the answer is x=4, y=6