Question

Show all work to solve the equation for x. If a solution is extraneous, be sure to identify it in your final answer. square root of the quantity x minus 2 end quantity plus 8 equals xsqrt(x-2+8) = x

Answer 1

We have that the equation is as follows:

`\sqrt[]{x-2+8}=x`

To solve this equation, we can proceed as follows:

1. Add the like terms in the radicand (-2 + 8 = 6):

`\sqrt[]{x+6}=x`

2. Square both sides of the equation:

`(\sqrt[]{x+6})^(^2)=x^2`

3. We already know that the square root of a number is like raising that number to the fraction 1/2. Then, we have - using the power to a power rule:

`((x+6)^{(1)/(2)})^2=(x+6)^{(2)/(2)}=(x+6)^1=x+6`

4. Therefore, we have:

`x+6=x^2`

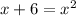
5. If we subtract x and 6 from both sides of the equation, we have:

`x-x+6-6=x^2-x-6\Rightarrow0=x^2-x-6`

6. Now, we have a second-degree (quadratic) polynomial that we can solve by factoring or by using the quadratic formula:

`x^2-x-6=0`

7. We can factor this polynomial if we find two numbers:

• a*b = -6

,

• a + b = -1

Then, both numbers are:

• a = 2

,

• b = -3

,

• a*b = 2 * -3 = -6

,

• a + b = 2 -3 = -1

Then, the above polynomial can be factored as follows:

`(x+2)(x-3)=0`

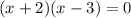
8. The solutions for this equation are:

`x+2=0\Rightarrow x=-2`

`x-3=0\Rightarrow x=3`

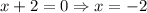
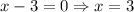
9. Now, to check these two solutions, we need to substitute these values into the original equation as follows:

For x = -2

`\sqrt[]{-2-2+8}=-2\Rightarrow\sqrt[]{-4+8}=-2\Rightarrow\sqrt[]{4}=-2\Rightarrow2\\e-2`

This is an extraneous solution. Although we got x = -2 as a solution to the resulting equation, it is not really a solution to the original equation. Therefore, x = -2 is an extraneous solution.

For x = 3

`\sqrt[]{3-2+8}=3\Rightarrow\sqrt[]{1+8}=3\Rightarrow\sqrt[]{9}=3\Rightarrow3=3`

Therefore, x = 3 is a solution to the original equation.

In summary, we have that the solution to the original equation:

`\sqrt[]{x-2+8}=x`

is x = 3.

There is an extraneous solution, x = -2 (it is not an actual solution to the original equation).