Question

#7 please, just checking work. p.s. if i am slow to reply it is because i have been doing homework for 10 hours

Answer 1

Given:

Center is

`(h,k)=(0,0)`

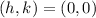
Vertices:

`(-3,0),(3,0)`

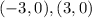
Co-vertices:

`(0,5),(0,-5)`

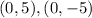
To find: The equation of hyperbola

Step-by-step explanation:

If the foci lie on the x-axis, the standard form of a hyperbola can be given as,

`(\mleft(x-h\mright)^2)/(a^2)-((y-k)^2)/(b^2)=1`

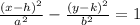
Where (h, k) is the center and a and b are the length of the semi-minor and semi-major axis.

Here,

Length of the major axis is,

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(5+5)^2+(0-0)^2} \\ =\sqrt[]{10^2} \\ =10 \end{gathered}`

Length of the minor axis is,

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(3+3)^2+(0-0)^2} \\ =\sqrt[]{6^2} \\ =6 \end{gathered}`

Therefore, the length of the semi-minor axis is a = 3 and the semi-major axis is b=5.

So, the hyperbola equation becomes,

`\begin{gathered} ((x-0)^2)/(3^2)-((y-0)^2)/(5^2)=1 \\ (x^2)/(3^2)-(y^2)/(5^2)=1 \end{gathered}`

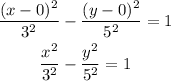
Final answer: The standard form of hyperbola equation is,

`(x^2)/(3^2)-(y^2)/(5^2)=1`