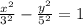Given:
Center is
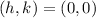
Vertices:
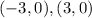
Co-vertices:
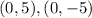
To find: The equation of hyperbola
Step-by-step explanation:
If the foci lie on the x-axis, the standard form of a hyperbola can be given as,
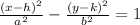
Where (h, k) is the center and a and b are the length of the semi-minor and semi-major axis.
Here,
Length of the major axis is,
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(5+5)^2+(0-0)^2} \\ =\sqrt[]{10^2} \\ =10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/eyg7xoo7x2lttyisx8bfvtzp2uw6l5yuqi.png)
Length of the minor axis is,
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(3+3)^2+(0-0)^2} \\ =\sqrt[]{6^2} \\ =6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nntex2ocu3am2ytm7k7ep53z33xcrljm7i.png)
Therefore, the length of the semi-minor axis is a = 3 and the semi-major axis is b=5.
So, the hyperbola equation becomes,
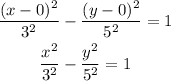
Final answer: The standard form of hyperbola equation is,