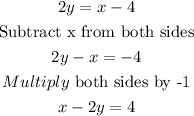Question

1. The equation of a line that goes through the point (0 - 4) and has a slope of 1/2 is? in slope intercept form and in standard form.

Answer 1

The equation of the line in slope-intercept form is:

`y=(1)/(2)x-4`

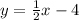
and in standard form is:

`x-2y=4`

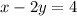
Step-by-step explanation:

The equation of a line in slope-intercept form is:

`y=mx+b`

where m is the slope, and b is the y-intercept.

Since the line passes through (0, -4), we can use this point to obtain the value of the y-intercept by sustituting x = 0, y = -4 and m = 1/2 into the equation of the line.

`\begin{gathered} -4=(1)/(2)(0)+b \\ \\ -4=b \end{gathered}`

Therefore, the equation of the line in slope-intercept form is

`y=(1)/(2)x-4`

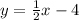
To write this in standard form, multiply both sides of the equation by 2

`\begin{gathered} 2y=x-4 \\ \text{Subtract x from both sides} \\ 2y-x=-4 \\ Multiply\text{ both sides by -1} \\ x-2y=4 \end{gathered}`