For finding if its a geometric sequence, we will do the quotient between a value of the sequence and the one before it. If we obtain the same number, this will be the common ratio.
For the terms 1 and 2:
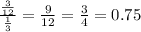
For the terms 2 and 3:
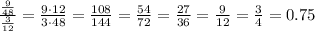
For the terms 3 and 4:
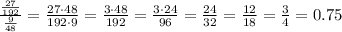
Finally, as all quotients give the same number, we conclude that the initial sequence is a geometric one, and that its common ratio is 0.75.