1 Answer

Chibuzo · Answer 1 · 2023-09-22T03:47:22+0000

We need to find the surface area of the given cylinder.

The surface area of a cylinder is the sum of the areas of the top and bottom bases and of the lateral surface.

The areas of the bases of a cylinder with radius r are, each, given by:

$\pi r²$

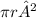
And the area of the lateral surface of a cylinder with a radius r and a height h is given by:

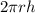
$2\pi rh$

Thus, the total surface area of a cylinder is:

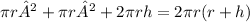
$\pi r²+\pi r²+2\pi rh=2\pi r(r+h)$

In this problem, we have:

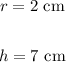
$\begin{gathered} r=2\text{ cm} \\ \\ h=7\text{ cm} \end{gathered}$

Thus, the surface area is given by:

$2\pi\cdot2\text{ cm}(2\text{ cm}+7\text{ cm})=4\pi(9\text{ cm})\text{ cm}=36\pi\text{ cm^^b2}$

Answer: 36π cm²

Please log in or register to add a comment.