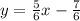Question

(A) Find the slope of the line that passes through the given points.(B) Find the standard form of the equation of the line.(C) Find the slope-intercept form of the equation of the line.(5,3) and (11,8)

Answer 1

Given that a line passes through points below

`\begin{gathered} (x_1,y_1)\Rightarrow(5,3)_{} \\ (x_2,y_2)\Rightarrow(11,8) \end{gathered}`

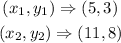
A) To find the slope, m, of a line, the formula is

`m=(y_2-y_1)/(x_2-x_1)`

Substitute the coordinates into the formula above

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(8-3)/(11-5)=(5)/(6) \end{gathered}`

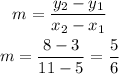
Hence, the slope, m, is 5/6

B) To find the equation of a line, the formula is

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ (y-3)/(x-5)=(5)/(6) \\ \text{Crossmultiply} \\ 6(y-3)=5(x-5) \\ 6y-18=5x-25 \\ 6y-5x=-25+18 \\ -5x+6y=-7 \end{gathered}`

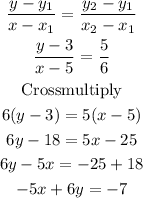
The standard form of an equation of a straight line is

`Ax+By=C`

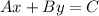
Hence, the equation of the line in standard form is -5x + 6y = -7

C) The slope-intercept form of the equation of a straight line is

`y=mx+b`

Make y the subject

`\begin{gathered} -5x+6y=-7 \\ 6y=5x-7 \\ \text{Divide both sides by 6} \\ (6y)/(6)=(5x-7)/(6) \\ y=(5)/(6)x-(7)/(6) \end{gathered}`

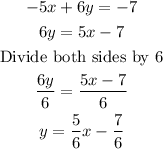
Hence, the equation of the line in slope-intercept form is

`y=(5)/(6)x-(7)/(6)`