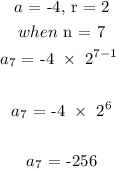Answer:
The 7th term is -256
Step-by-step explanation:
Given:
-4,-8, -16, . . .
To find:
The 7th term in the sequence
We were not informed the type of sequence, we need to check if it has a common difference or common ratio
common difference (d) = next term - previous term
d = -8 - (-4) = -8 + 4 = -4
d = -16 - (-8) = -16 + 8 = -8
No common difference
Common ratio (r) = next term/previous term
r = -8/-4 = 2
r = -16/-8 = 2
The ratio is common. Hence, it is a geometric sequence
To get the 7th term, we will apply the formula: