ANSWER
x = 5
Step-by-step explanation
As shown in the figure, the two segments from C to the intersection with AB and from the intersection to D are congruent. This means that they have the same length:
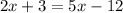
We have this equation that we can solve for x.
First we need that all the terms that contain x are on the same side of the equation. Subtract 2x from both sides:
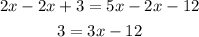
Now we need that all the terms that don't contain x on the same side as well. Add 12 on both sides of the equation:
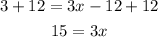
Finally, to find x, divide both sides by 3:
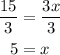
The value of x is 5.