Find the equation of the line which passes through the point(10,6) And is parallel to the given line. Express your answer in a slope intercept form simply check your answer

Question

asked Aug 16, 2023 180k views

1 Answer

Cecchi · Answer 1 · 2023-08-20T11:30:59+0000

Given:

Equation of line:

Line pass ( 10,6) and parallel to a given line

Find-:

Equation of another line.

Explanation-:

Given line is:

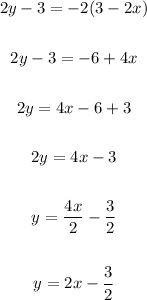
$\begin{gathered} 2y-3=-2(3-2x) \\ \\ 2y-3=-6+4x \\ \\ 2y=4x-6+3 \\ \\ 2y=4x-3 \\ \\ y=(4x)/(2)-(3)/(2) \\ \\ y=2x-(3)/(2) \end{gathered}$

Compared with the general form of the equation:

Where,

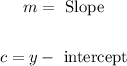
$\begin{gathered} m=\text{ Slope} \\ \\ c=y-\text{ intercept} \end{gathered}$

Then

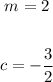
$\begin{gathered} m=2 \\ \\ c=-(3)/(2) \end{gathered}$

The slope of a line is 2 so the slope of the parallel line is also the same then the equation becomes:

$\begin{gathered} y=mx+c \\ \\ y=2x+c \end{gathered}$

For the value of "c"

Line pass (10,6) then,

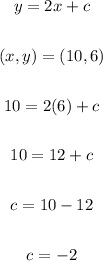
$\begin{gathered} y=2x+c \\ \\ (x,y)=(10,6) \\ \\ 10=2(6)+c \\ \\ 10=12+c \\ \\ c=10-12 \\ \\ c=-2 \end{gathered}$

So, equation of parallel line is:

$\begin{gathered} y=mx+c \\ \\ y=2x-2 \end{gathered}$