We know that the distance he covers increases by 10% each day.
Then, being an the distance covered in day n, we have the recursive equation:
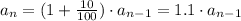
This is a geometric series with r = 1.1.
It will have the explicit formula:
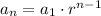
If after 7 days, the total distance travelled is 75897 miles, we can use the formula for the sum of terms in geometric series like this:
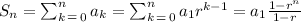
As we know that when n = 7, Sn = 75897 and r is r = 1.1, we can find a1 as:
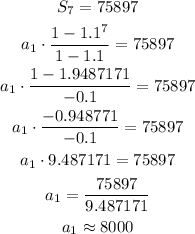
Then, we can now use a1 to find a complete expression for Sn:
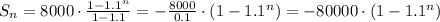
We can test this for n = 7:
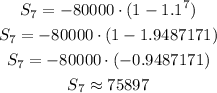
Answer: the expression for the sum of n terms, Sn, is Sn = -80000*(1 - 1.1^n)