Question

Hello! A little stuck on parts a, b, and c. Thanks!

Answer 1

Consider the function

`\begin{gathered} f(t)=Acos(Bt+C)+D \\ A\rightarrow\text{ amplitude} \\ B\rightarrow period=(2\pi)/(B) \\ C\rightarrow horizontal\text{ shift} \\ D\rightarrow\text{ vertical shift} \end{gathered}`

The period of the function is 20 seconds; then,

`\begin{gathered} (2\pi)/(B)=20 \\ \Rightarrow B=(\pi)/(10) \end{gathered}`

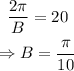
On the other hand, the distance from the highest to the lowest point is 4 feet; thus,

`\begin{gathered} A=(4)/(2)=2 \\ \Rightarrow A=2 \end{gathered}`

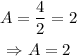
The answers to part A) are amplitude=2ft and period=20 seconds.

On the other hand, the average height of the function is equal to its midline which is located at y=10, according to the question. Then,

`D=10`

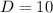
So far, the function that models the problem is

`\begin{gathered} f(t)=2cos((\pi t)/(10)+C)+10 \\ \end{gathered}`

B) Given that the height of the bottle is equal to 10 at t=0,

`\begin{gathered} f(0)=10 \\ \Rightarrow cos(C)=0 \\ \Rightarrow C=\pm(\pi)/(2) \end{gathered}`

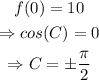
Furthermore, after t=0 the bottle moves upwards; then, C=-pi/2.

Then, the function that represents the situation is

`\Rightarrow f(t)=2cos((\pi t)/(10)-(\pi)/(2))+10`

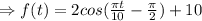
C) The graph of the function is

According to the graph, after 15 seconds, the function will reach its lowest height.