Question

Find the total surface area of this cone.Leave your answer in terms of 7.24in-10 inSA = [ ? ]in?Hint: Surface Area of a Cone = tre + BWhere e = slant height, and B = area of the base

Answer 1

Surface area of a cone:

`\begin{gathered} SA=\pi\cdot r\cdot l+B \\ SA=\pi\cdot r\cdot s+\pi\cdot r^2 \\ r=\text{ radius} \\ l=\text{slant height} \end{gathered}`

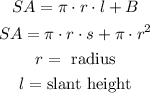
For the given cone:

As you have the height of the cone and not the slant height. Use the Pythagorean theorem to find the hypotenuse in the right triangle formed by the radius and slant height:

`\begin{gathered} h^2+r^2=l^2 \\ \\ l=\sqrt[]{h^2+r^2} \\ l=\sqrt[]{(24in)^2+(10in)^2} \\ l=\sqrt[]{576in^2+100in^2} \\ l=\sqrt[]{676in^2} \\ l=26in \end{gathered}`

Find the surface area:

`\begin{gathered} SA=\pi\cdot10in\cdot26in+\pi\cdot(10in)^2 \\ SA=260\pi in^2+100\pi in^2 \\ SA=360\pi in^2 \end{gathered}`

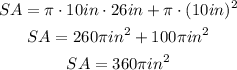
Then, the surface area of the given cone is 360π square inches