Question

For each system of linear equations shown below, classify the system as "consistent dependent," "consistent Independent," or "inconsistent." Then, choose thbest description of its solution. If the system has exactly one solution, give its solution.System ASystem BSystem

Answer 1

A system of the linear equation can be consistent independent, consistent dependent, or inconsistent depending on its solution.

System A :

We have the equations:

`\begin{gathered} y\text{ = -2x - 3 (line 1)} \\ y\text{ = -2x + 1 (line 2)} \end{gathered}`

We can see that the lines have a similar slope, hence they are parallel. This is shown on the graph.

Hence, the system of equations is inconsistent.

This means that the system has no solution.

System B

We have the equations:

`\begin{gathered} y\text{ = 2x (line 1)} \\ y\text{ = }(1)/(2)x\text{ - }(3)/(2)\text{ (line 2)} \end{gathered}`

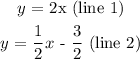
From the graph, the lines intersect at only one point (-1, -2).

Hence, the system of equations is consistent independent

This means that the system has a unique solution

Solution : (-1, -2).

System C

We have the equations:

`\begin{gathered} y\text{ = }-3x\text{ (line 1)} \\ 3x\text{ + y = 0 (line 2)} \end{gathered}`

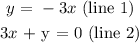
Re-writing the equation for line 2, we have:

`\begin{gathered} y\text{ = -3x (line 1)} \\ y\text{ = -3x (line 2)} \end{gathered}`

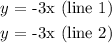
From the graph, one line lies on top of the other.

Hence, the system of equations is consistent dependent.

This means that the system has infinitely many solutions.