Question

Use Part ofthe Fundamental Theorem of Calculus to find che derivative of the function

Answer 1

The fundamental theorem of calculus states that if f is a continuous real-valued function defined in a closed interval [a,b], and F is the function defined on [a,x] by

`F(x)=\int ^x_af(t)dt`

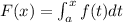
Then, F is uniformly continuous on [a,b] and differentiable on (a,b), and

`F^(\prime)(x)=f(x);x\in(a,b)`

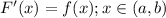
In our case,

`f(t)=(1)/(3)(t^2+\sqrt[]{t})`

is continuous in the interval (0,infinite); so, it is continuous in [2,infinite)

Therefore,

`\Rightarrow F(x)=\int ^x_2(1)/(3)(t^2+\sqrt[]{t})dt`

Thus,

`\Rightarrow F^(\prime)(x)=(1)/(3)(x^2+\sqrt[]{x})`

The answer is F'(x)=(x^2+sqrt(x))/3