Question

Hi Please help me this is due today and I don't understand anything. Please help Q: Find the Missing Variable in the following triangles.

Answer 1

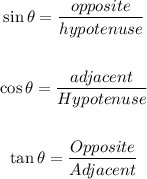
We are given a right triangle. We are asked to determine the unknown side. In any right triangle, we have a 90 degrees angle that is represented with a small square. The side that is in front of the 90 degrees triangle is called the "hypotenuse".

Now. When we consider one of the other two angles we're gonna have two sides. The side that "touches" the angle we are considering is called the "adjacent side" and the side in front of the angle we are considering is called the "opposite side. We can see this in the following diagram:

Here we are considering angle A, and therefore, we have an adjacent side that is the one that touches angle A and the opposite side the one in front of angle A.

If we consider the other angle then we would have:

Here we are using angle B, therefore, from this perspective, the adjacent side is the one that touches angle B and the opposite side is the one in front of angle B.

When we are asked to determine a side given an angle and another side we must use a trigonometric function. The three most important are Sine, Cosine, and Tangent. They are defined as follows:

`\begin{gathered} \sin \theta=(opposite)/(hypotenuse) \\ \\ \cos \theta=(adjacent)/(Hypotenuse) \\ \\ \tan \theta=(Opposite)/(Adjacent) \end{gathered}`

Therefore, we need to use a function that relates the known side with the unknown side.

For part A, the known side is the opposite side of the 45 degrees angle and the unknown side is the hypotenuse, therefore, we need to use sine.

`\sin 45=(opposite)/(hypotenuse)`

Substituting we get:

`\sin 45=(28)/(m)`

Now, we solve for "m" first by multiplying both sides by "m":

`m\sin 45=28`

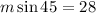
Now we divide both sides by "sin45":

`m=(28)/(\sin 45)`

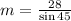
The value of "sin45" is given by:

`\sin 45=\frac{1}{\sqrt[]{2}}`

Substituting we get:

`m=\frac{28}{\frac{1}{\sqrt[]{2}}}`

Now we simplify:

`m=28\sqrt[]{2}`

And thus we have determined the side "m".

For par D, we are given and angle of 45 degrees and the opposite and adjacent sides. We can use a trigonometric function that relates the opposite side with the hypotenuse or the adjacent side with the hypotenuse and we would get the same result no matter which one we choose.

Let's choose sine and we get:

`\sin 45=\frac{30\sqrt[]{2}}{j}`

Now we solve for "j" using the same procedure that we used before and we get:

`j=\frac{30\sqrt[]{2}}{\sin 45}`

Since we know that:

`\sin 45=\frac{1}{\sqrt[]{2}}`

We substitute this and we get:

`j=\frac{30\sqrt[]{2}}{\frac{1}{\sqrt[]{2}}}`

Simplifying:

`j=30\sqrt[]{2}(\sqrt[]{2})`

Solving the product:

`j=30(\sqrt[]{2})^2=30(2)=60`

Therefore, the value of the hypotenuse is 60.