Given:
The length of the longer leg of a right triangle is 6ft more than twice the length of the shorter leg.
The length of the hypotenuse is 9 ft more than twice the length of the shorter leg.
Step-by-step explanation:
To calculate longer length:
Consider the shorter leg as s and longer leg as l.
As the longer leg of a right triangle is 6ft more than twice the length of the shorter leg, the longer leg can be represented as,
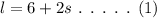
To calculate hypotenuse:
Now, consider the hyptenuse as h,
As the hypotenuse is 9 ft more than twice the length of the shorter leg, the hypotenuse can be represented as,

To calculate shorter leg:
Using Pythagorean theorem, the shorter leg can be calculated as,
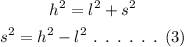
On plugging the equation (1) and (2) in equation (3),
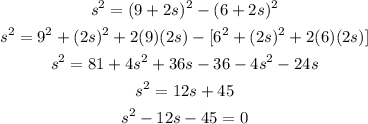
On solving the above quadratic equation,
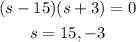
Since negative length is not a possible values, the value of shorter length of the right triangle is, s = 15 ft.
Substitute in equation (1):
On plugging the value of s in equation (1),
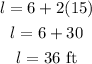
Substitute in equation (2):
On plugging the value of s in equation (2),
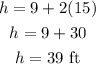
Hence,
Length of the shorter leg: 15 ft.
Length of the longer leg: 36 ft.
Length of the hypotenuse: 39 ft.