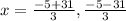Given the function:
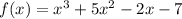
The critical points are points where the derivative of the function is zero. So, first we find the derivate of the function:
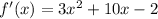
The derivative equals zero and we find the values for x:
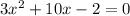
We use the general formula for quadratic equations, where:
a = 3
b = 10
c = -2
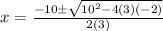
Simplify:
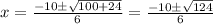
Separate the solutions:
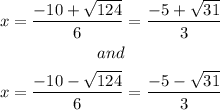
Answer: the critical points are: