As the problem suggests, we must do h = 0, then we must solve the following quadratic equation
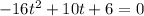
We can simplify it to (divide all terms by 2)
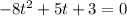
Now we can use the quadratic formula to solve it
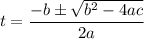
Where
a = -8
b = 5
c = 3
Then
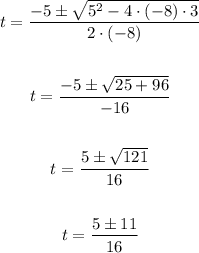
Therefore the solutions are
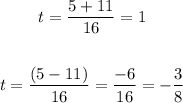
The only valid solution is t = 1, because we can have negative time, therefore the answer is t = 1
Final answer: